Линейный факторный анализ. Метод главных компонент
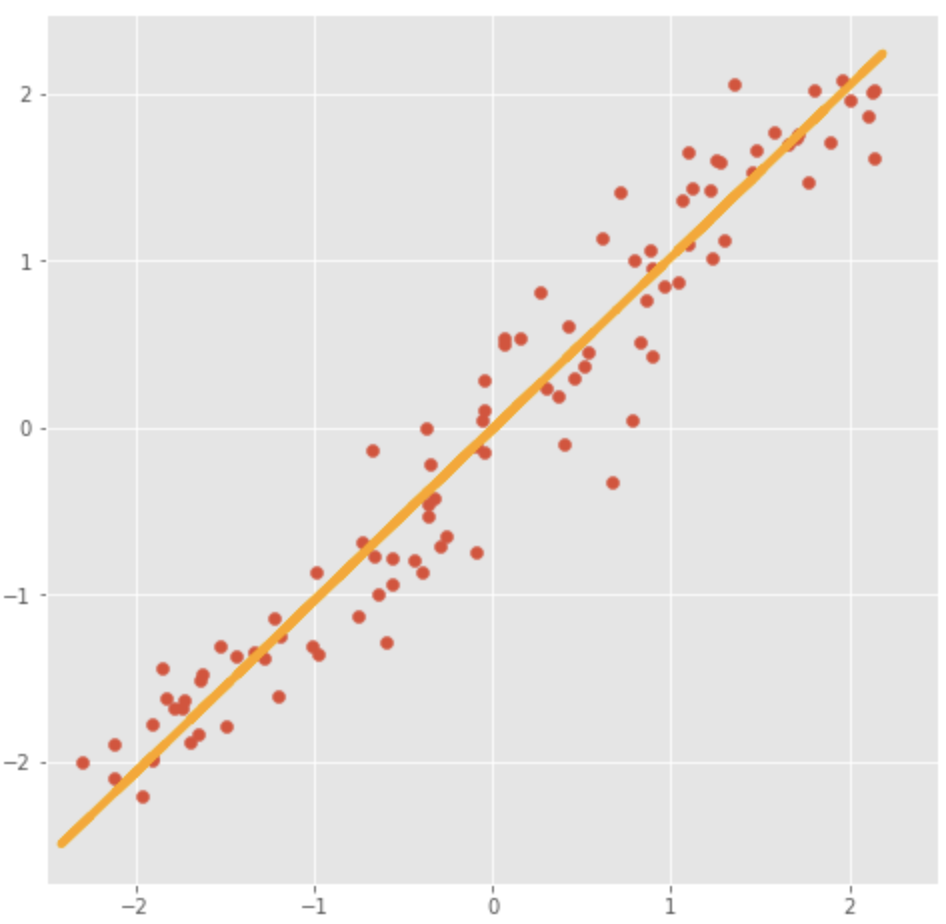
Сгенерируем данные на плоскости и попробуем их обяснить
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
x1 = np.linspace(-2.2, 2.2, 100)
fx = linfun(x1)
dots = np.vstack([x1, fx]).T
noise = 0.2 * np.random.randn(*dots.shape)
dots += noise
pca = PCA(1)
# 1 - это количество компонент которое мы хотим получить
# Так как у нас все точки лежат на одной прямой, то одной координаты будет достаточно
pca_coords = pca.fit_transform(dots)
print('Доля объясненной вариации данных=', round(pca.explained_variance_ratio_[0]*100, 2))
print('Кординаты вектора главного компонента=', pca.components_[0])
# Доля объясненной вариации данных= 99.04
# Кординаты вектора главного компонента= [-0.71045377 -0.70374387]
# Восстановление данных по главному компоненту
pdots_pca = pca.inverse_transform(pca_coords)
vpdots = pdots_pca[idxs]
# Визуализация
plt.figure(figsize=(8, 8))
plt.xlim([-2.5, 2.5])
plt.scatter(dots[:, 0], dots[:, 1], zorder=1)
plt.plot(pdots_pca[:,0], pdots_pca[:,1], color='orange', linewidth=4, zorder=4)