Метод градиентнго спуска

Геометрическая интерпретация вектора градиента

Градиент функции f(x,y) в точке (x0,y0) – это вектор, координаты которого равны частным производным функции f(x,y) в точке (x0,y0)

\[\bar{g}=(f^{'}_{x}(x_{0},y_{0}), f^{'}_{y}(x_{0},y_{0}))\]

Вектор градиента можно использовать для вычисления производной функции f(x,y) по любому направлению:

\[\frac{df(x,y)}{d\bar{p}}=\bar{g}\cdot \bar{e_{p} }\] \[\bar{e_{p}}=\frac{\bar{p}}{\left|\bar{p}\right|}\]

Основной геметрический смысл вектора градиента:

Он показывает направление наибыстрейшего возрастания функции
Величина (евклидова длина) вектора градиента равна производной функции вдоль направления градиента и является максимальной производной из всех производных по направлению

\[\frac{df(x,y)}{d\bar{p}}=\left|\bar{g}\right| \cdot \left|\bar{e_{p} } \right| \cdot \cos (\widehat{\bar{g} \cdot \overline{e_{p} } } ) = \left|\bar{g}\right| \cdot \cos (\widehat{\bar{g} \cdot \overline{p } } )\]

Программное решение

import numpy as np
import matplotlib.pyplot as plt

def grad_desc(g, r, alpha=0.01, eps_g = 0.1, maxiters=100):
    iter = 0
    trace = [r]
    while (np.linalg.norm(g(r[0],r[1])) > eps_g) and (iter < maxiters):
        r = r - alpha * g(r[0],r[1])
        trace.append(r)
        iter += 1
    return trace

x = np.linspace(-3, 3, 20)
y = np.linspace(-3, 3, 20)
X,Y = np.meshgrid(x,y)
f = lambda x,y: x**2 + 4*y**2 +x
g = lambda x,y: np.array([2*x+1, 8*y])
Z = f(X,Y)

# Определим точку (x0, y0)
r0 = np.array([1, -2.5])
x0, y0 = r0
# зададим коэффициент шага
alpha = 0.01
# выполним оптимизацию
trace = grad_desc(g, r0, alpha=alpha)
trace = np.array(trace).T

fig = plt.figure()
ax = plt.axes(projection='3d')

surf =ax.contourf(X, Y, Z, 30, )
TX = trace[0]
TY = trace[1]
TZ = f(TX,TY)
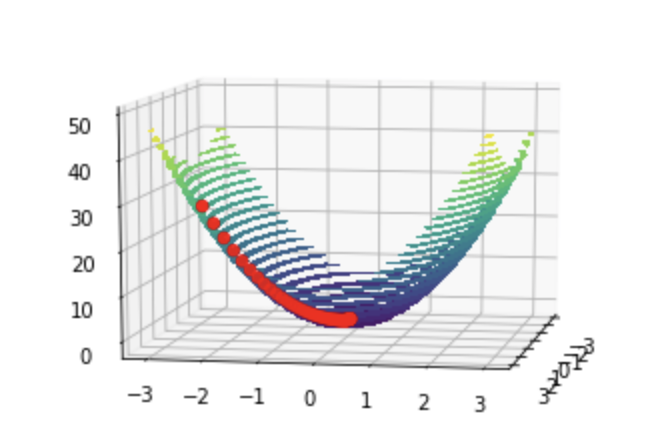
ax.scatter(TX, TY, TZ, s=30, c='r')
ax.view_init(10, 10)
fig.show()

Метод градиентного спуска