Линейный регрессионный анализ

Определение:

К задачам регрессионного анализа данных относятся задачи, в которых на основании ранее полученных данных наблюдения требуется построить зависимости одних показателей от других.

Задачу построения линейной регрессии с использованием критерия наименьших квадратов можно записать в следующем виде:

\[\left\|X * \bar{a} - Y \right\| _{2} \rightarrow \min\]

Нормальная система уравнений

\[X^{T} * X * \bar{a} = X^{T} * Y\]

Пример прогноза

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn import metrics

csv_file_path = dir_path + "файл_с_исходными_данными.csv"
data = pd.read_csv(csv_file_path, sep=';')
XY = data.values
Xm = XY[:,:-1]
Y = XY[:,-1:]

# Разделяем полученные данные на тестовые и тренировочные
x_train, x_test, y_train, y_test = train_test_split(Xm, Y, train_size=0.7, random_state=42) 

lin_reg = LinearRegression()
model = lin_reg.fit(x_train, y_train)

print('a0=', model.intercept_)
print(model.coef_)

# Для примера:
# a0= [-0.57]
# [[1.17 0.95 2.07 3.1 ]]

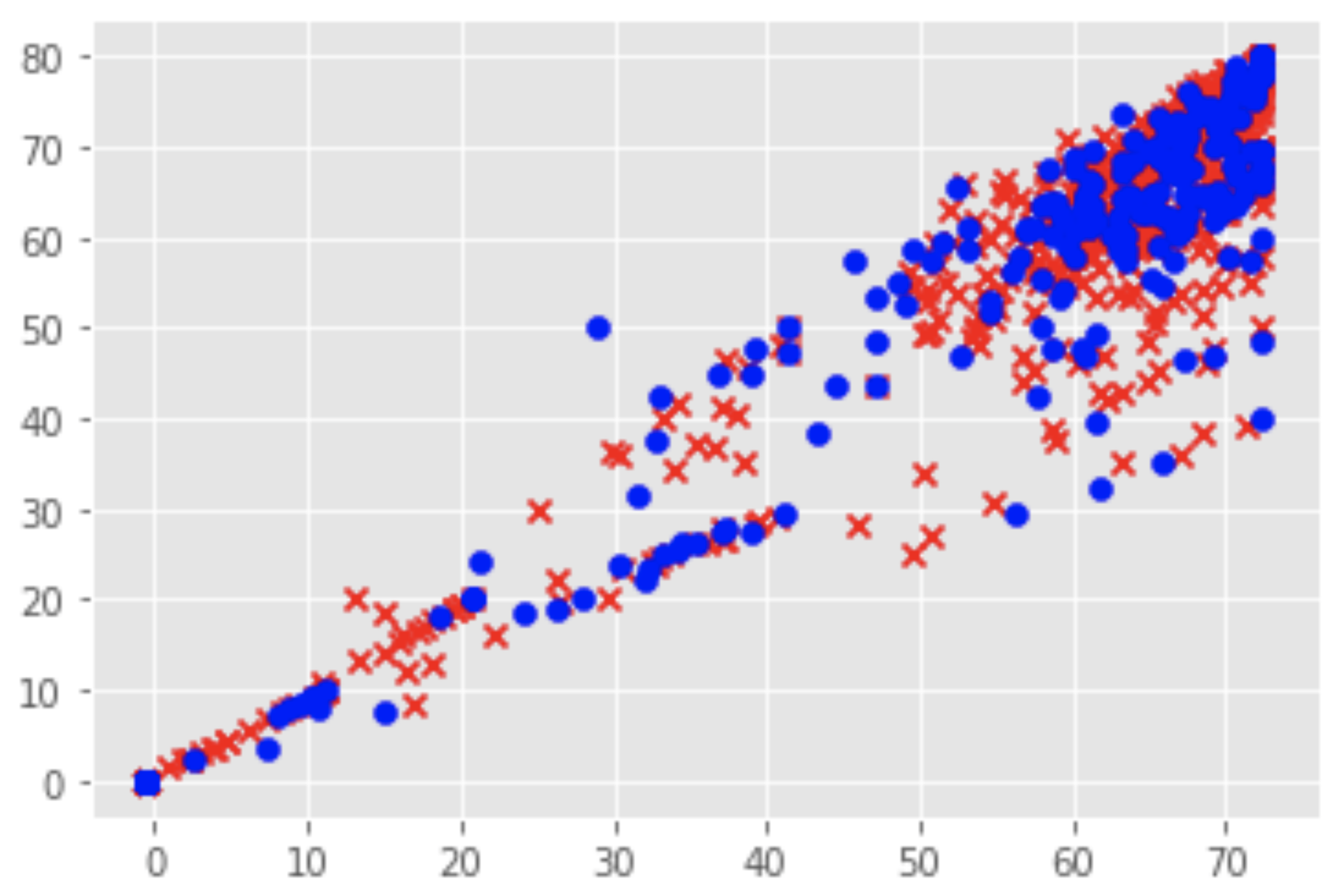
plt.scatter(x_train @ model.coef_[0] + model.intercept_, y_train, c='r', marker='x')
plt.scatter(x_test @ model.coef_[0] + model.intercept_, y_test, c='b', marker='o')

# model.predict(x_test) == x_train @ model.coef_[0] + model.intercept_ <- для примера

Пример построения линейной регрессии

** Метрики **

y_predicted = model.predict(x_test)
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_predicted))
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_predicted))
print('r2_score:', metrics.r2_score(y_test, y_predicted))

# Mean Absolute Error: 4.800584118066579
# Mean Squared Error: 49.19797455157672
# r2_score: 0.9335753945516053